Much like humans, crystalline materials are defined by their defects. Within a single crystal defects are typically small clusters of additional or missing atoms or lines of broken atomic bonds known as dislocations.
Under an applied stress, it is the movement of defects that determine the mechanical response of the crystal. As defects interact strongly with thermal vibrations, it is well known that their motion is typically viscous, with a velocity proportional to the applied force. The constant of proportionality is known as the drag, or friction, parameter.
Since the pioneering work of Liebfried and Nabarro in the 1950s there have been many attempts to calculate the drag parameter by considering how a crystal defect scatters thermal phonons. As the phonon dispersion is linear, and the dislocation dispersion is quadratic, a slowly moving dislocation cannot absorb or emit a single phonon and thus the scattering processes involve at least two phonons. It turns out that this gives a predicted drag parameter that rises at least linearly with temperature. This widely used result has an intuitive appeal, as it implies the viscosity of the phonon gas surrounding a defect increases with temperature.
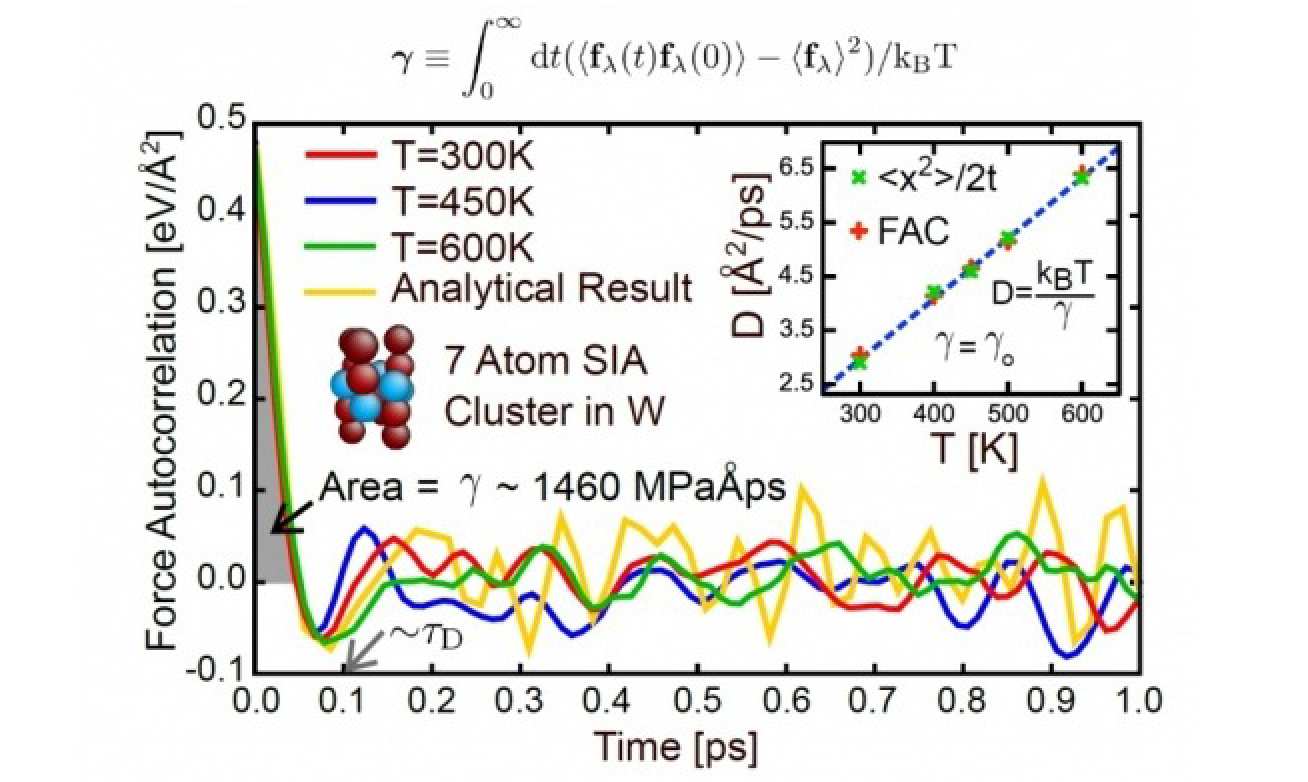
However, since their emergence in the 1990s, atomistic simulations of drifting and diffusing defects have found that the drag parameter is often independent of temperature, completely at odds with the results of phonon scattering theory. In a recent issue of Physical Review Letters [1] Tom Swinburne (TSM-CDT cohort 2), under supervision from Prof Adrian Sutton FRS and Prof Sergei Dudarev derived a new expression for the drag parameter, using Zwanzig's projection technique to treat defect motion as a transformation of the crystal rather than a physical object moving in a gas of phonons. This approach shows that phonon scattering approaches erroneously assume defects and phonons have separately conserved momentum, whereas in a real crystal the normal modes are intimately correlated with defect motion. Because of this the phase space restrictions inherent to a scattering approach do not apply, thus allowing a temperature independent drag parameter. A computational implementation of the developed theory shows excellent agreement with more expensive trajectory analysis methods of calculating the drag parameter. Future work will focus on extending the theory to understand the role of thermal fluctuations in a wide range of crystal plasticity phenomena.
[1] T.D. Swinburne, S.L. Dudarev and A.P. Sutton, Physical Review Letters 113, 215501, 2014