Atom chips are micro-fabricated, integrated devices that use electric, magnetic and/or optical fields to confine and manipulate cold atoms. The flexible and accurate control of cold atom clouds and Bose-Einstein condensates (BECs) that can be achieved with these devices makes them ideal for atom interferometry. Such a chip-based atom interferometer has many applications, ranging from fundamental studies of coherence and squeezing during the splitting process to 1D Bose gases and quantum metrology.
Our atom chip is made by evaporating a 3 µm layer of gold onto a silicon substrate. Multiple wires are patterned into this layer by ion-beam milling. The reflective gold surface is also used to make a mirror magneto-optical trap (MOT).
The geometry of the wires is designed to create an elongated Ioffe-Pritchard magnetic trap. The multiple parallel wires allow a single trapping potential to be split into two (or more) traps, forming the analogue of an optical beam splitter.
We load a mirror MOT from a cold atomic beam produced by a low-velocity intense source (LVIS). From there we transfer the atoms into a magnetic trap formed by running current through the chip Z-wires and controlling external bias fields. The cloud is then cooled to BEC via radio-frequency forced evaporation. We typically produce a BEC with up to 106 atoms in this trap.
Atom Chip Inteferometry
Following recent advances in techniques for manipulating atoms using an atom chip, we split our BEC using an adiabatic radio-frequency (RF) double-well potential. The characteristics of the system are determined by the distance between the wells d, the height of the barrier u0 and the number of atoms in the condensate.
The RF signal is directly coupled onto the two trapping wires. A splitting of the BEC can be achieved either by ramping up the RF-power or by a sweep of the RF frequency. The later allows us big trap separations where the two clouds can be imaged in-trap. The phase between the two RF-currents determines the splitting direction. We usually use a horizontal splitting configuration preparing atoms in an equal gravitational potential.
To get sensitive control of the splitting we ramp up the RF-power of our oscillator, with which we achieve well separations between 3μm and 4μm. This is just above the threshold where the two clouds separate.
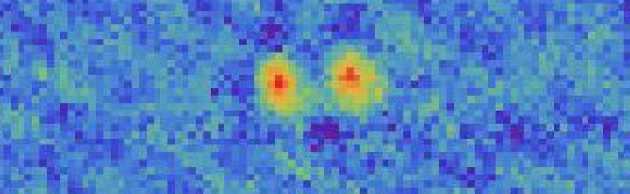
Splitting the BEC into two wells is directly equivalent to a beam splitter. By releasing the clouds and allowing them to overlap in time-of-flight (TOF) we observe interference of the atoms which results in a distinctive modulation of the density of the overlapping components, the so-called interference fringes. To understand the origin of this pattern we can think of the two wells as the two coherent sources in the double slit experiment. A phase can be assigned to every BEC which leads to the occurrence of matter wave interference.
The wavelength of these interference fringes is inversely proportional to the initial splitting distance in the double well potential. The relative phase of the two components can be read out directly from the fit to the interference fringes.
In the picture an image of a single interference experiment after 12ms TOF is shown. All interesting parameters like phase and wavelength are determined by fitting a model to the pattern.
Observing interference, however, does not yet make an interferometer. To make an efficient measurement we need to prepare the cloud in a stable way and reproducible way.
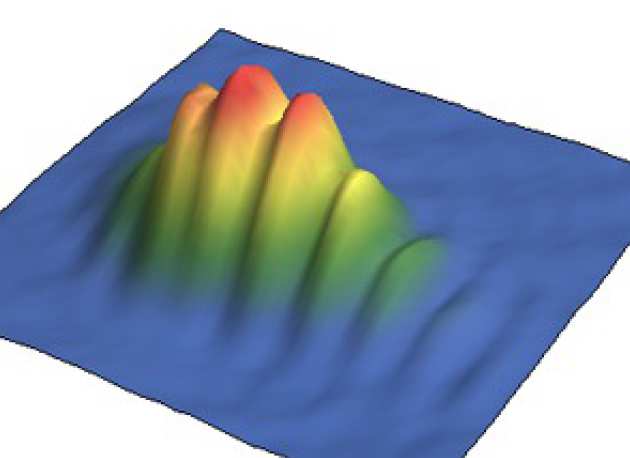Atoms are coupling quite sensitive to magnetic, electric and gravitational fields. However, to measure one of these, it is necessary that the relative phase is stable. That means doing the same experiment with the same parameters over and over again should always give the same relative phase.
The image on the right shows the averaged image of 100 equal experiments. We see immediately that the phase is not random due to a distinct fringe pattern.
In the real world there will always be a range over which the phase is spread because there is an uncertainty principle between number and phase difference of the two wells. But by repeating the experiment we can extract a particular mean value for the relative phase.
We have measured the evolution of this phase spread. Whereas the spread is quite narrow directly after the splitting process, it is around π after a hold time of 5ms inside the trap. After 10ms time the phase is more or less random.
After splitting the clouds are in a binomial state which can be described by a superposition of number states. The number states have all a different phase evolution causing the circular standard deviation Δφ to evolve linearly in time.
We can conclude from this section that an interferometric measurement is limited to around 5ms interaction time, because at larger times a determination of phase is no longer possible. This, however, is quite long as the atoms are coupling very sensitive to various fields.
Please contact Eoin Butler, Iain Barr or Ben Yuen