We tackle a wide variety of problems at the forefront of interdisciplinary applied mathematics and engineering science fundamentals. We focus on complex, multiphase systems, using cutting-edge analytical and computational tools to develop a generic fundamental understanding of systems for which there is currently no existing theory.
Each of these projects is overseen by Professor Serafim Kalliadasis. Listed below are other current and former group members and collaborators with expertise in these areas. These projects are currently ongoing and are funded by a variety of EPSRC, ERC and EU grants. Our publications page contains details of our contributions. You can also read about some of our recent research highlights.
| Title | Collaborators - contributors |
|---|---|
| Data-driven modelling of the electricity day-ahead markets | Mr Antonio Malpica-Morales, Dr Miguel A. Durán-Olivencia |
| Physics-informed Bayesian inference of external potentials in classical density functional theory | Mr Antonio Malpica-Morales, Dr Peter Yatsyshin, Dr Miguel A. Durán-Olivencia |
| Surface nanodrops and nanobubbles: a classical density functional theory study | Dr Peter Yatsyshin |
| Unconditional bound-preserving and energy-dissipating finite-volume schemes for the Cahn-Hilliard equation | Dr Rafael Bailo, Prof José A. Carrillo, Dr Sergio P. Perez |
| Please use the menu below to see some results from our recent projects | |
Summaries of selected projects
- Data-driven modelling of the electricity day-ahead markets
- Physics-informed Bayesian inference of external potentials in classical density functional theory
- Surface nanodrops and nanobubbles: a classical density functional theory study
- Unconditional bound-preserving and energy-dissipating finite-volume schemes for the Cahn-Hilliard equation
Obtaining a mathematical representation of electricity prices is the cornerstone of the decision-making process in a liberalised electricity market landscape. Over the last few years, the electricity day-ahead price has become a signal of market behaviour. Traditional approaches of electricity day-ahead price modelling rely upon one-dimensional diffusion processes or multidimensional autoregressive models. Both mathematical formulations provide an explicit and reliable short-term price representation. However, these state-of-the-art models rely heavily on prior assumptions in order to accurately describe some of the day-ahead price features. This approach to day-ahead price representation is elaborate, requiring good domain knowledge and practice based on a constellation of experiences interpreted judiciously.
Our overarching objective is the conceptualisation and formulation of a framework accounting for the stochastic nature and the most widely-known features of the day-ahead prices without any prior domain knowledge. We propose that the electricity day-ahead price is the solution of a multivariate generalised Langevin equation (GLE). Each dimension of the GLE represents a single time block auctioned in the market. The drift and diffusion terms governing the GLE are obtained by a data-driven technique coupled with the definition of the Kramers-Moyal coefficients. The framework is exemplified with empirical data from the Spanish electricity day-ahead market from the period 2004-2020, although it is sufficiently general to be applied to any electricity-market system. The results reveal finer details of the price behaviour, such as equilibrium prices and mean-reversion effects. Not surprisingly, the observed price behaviour arises from the purely data-driven technique without imposing any prior assumption. All in all, the formulated GLE offers a reliable price representation of the Spanish day-ahead market in abscence of exogenous effects, i.e., assuming stationary conditions.
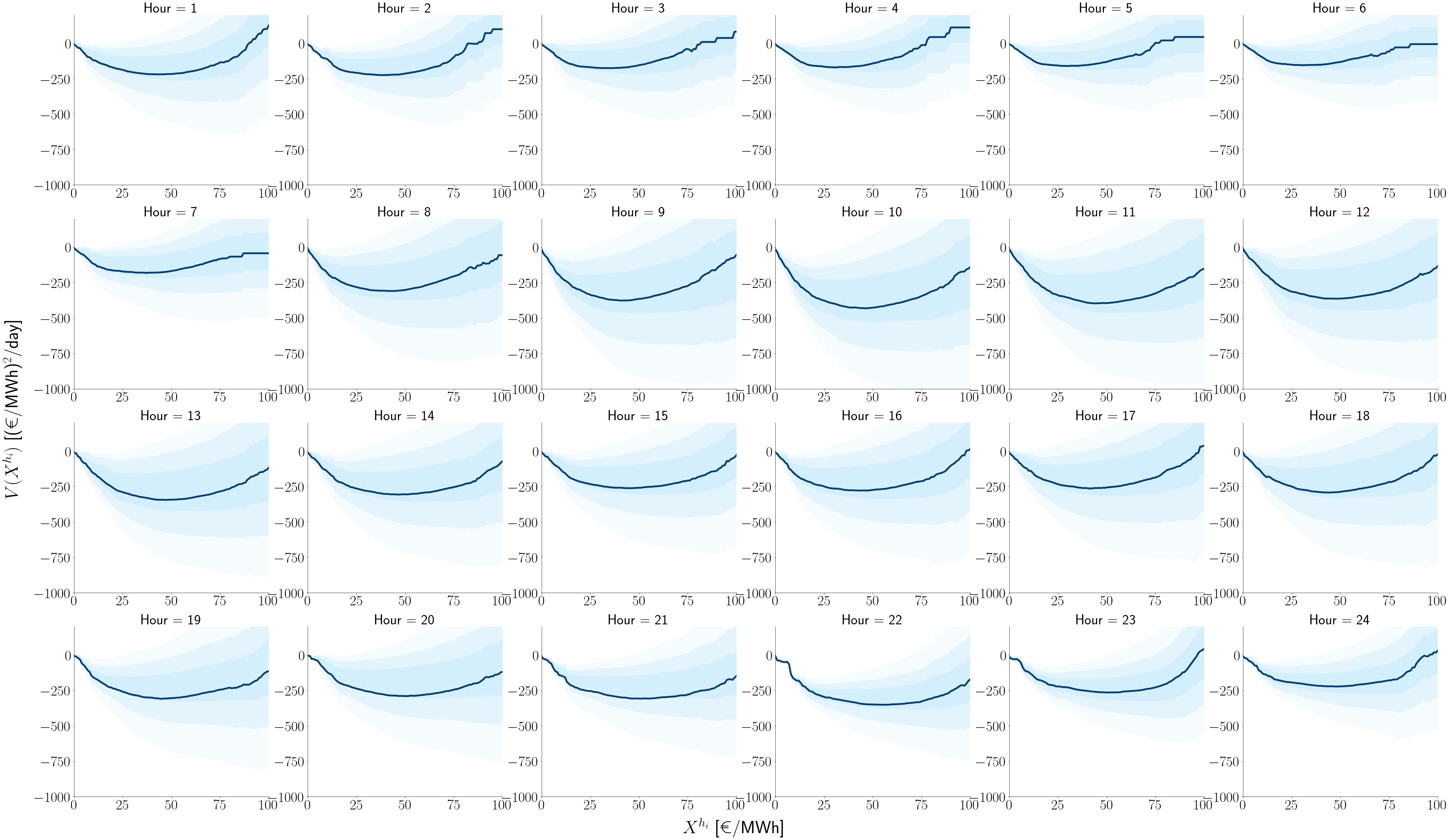
Particle model for the electricity day-ahead price: potential function of each hour obtained from the drift term. Dark-blue lines represent the expected potential. Each hour exhibit different different equilibrium values (minimum of the parabola) and distinct mean-reverting intensity values. These dynamics are reminiscent of a particle fluctuating in a harmonic potential.
The theoretical-computational framework proposed here can serve as the starting point and backbone for further model refinement and enhancement. Of particular interest would be extending our stationary formulation to non-stationary conditions leading to the development of forecasting models. These enhanced models will be able to capture external forces responsible for large electricity price deviations with respect to past equilibrium prices. We also believe that, because of its generality, versatility and seamless replicability, our framework can be adopted by a broad spectrum of communities, from applied mathematics to energy modelling and economics. For instance, it would be interesting to infer hidden price-related dynamics from other markets (natural gas, CO2 emissions, electricity balancing markets) and/or distinctly different market configurations.
Classical density-functional theory (DFT) is a statistical-mechanical framework which states that the free energy of a many-particle system can be written as a functional of the particle density. Under such circumstances, the system’s equilibrium is determined by the extrema of the free-energy functional, which represent the density profiles at equilibrium.
The employment of classical DFT to obtain the equilibrium particle-density might be a challenging task if system particles interact through fine detailed potentials or there exist an external potential, acting on the many-particle system. External fields might modify the mechanical, electrical or optical properties of porous media in equilibrium with a bulk fluid having profound impacts on fields such as separation processes, crystallization or nanofluidics, to name a few.
We introduce a statistical-learning framework to infer the external potential exerted on a classical many-particle system. We combine a Bayesian inference approach with the classical DFT apparatus to reconstruct the external potential, yielding a probabilistic description of the external-potential functional form with inherent uncertainty quantification. Our framework is exemplified with a grand-canonical one-dimensional classical particle ensemble with excluded volume interactions in a confined geometry, reminiscent of a fluid inside a pore.
The required training dataset is generated using a Monte Carlo (MC) simulation where the external potential is applied to the considered grand-canonical ensemble. The resulting particle coordinates from the MC simulation are fed into the learning framework to uncover the external potential. This eventually allows us to characterize the equilibrium density profile of the system by using the tools of the DFT.

Illustration of the external potential inference for two different datasets, D800 (800 particle configurations) and D6000 (6,000 particle configurations). Left: Comparison between the predicted external potential distribution and the exact external potential (red line). The grey areas encloses the [1st, 99th] percentiles of the predictive distribution. Right: Representation of the exact density profile obtained from DFT of the grand-canonical one-dimensional ensemble (red line), the predicted mean density profile distributions for D800 (black solid line) and D6000 (black dash line) and the histogram of D800 used to infer the external potential.
Our Bayesian formulation enables accurate and efficient identification of the external potentials for the prototypical case study of a fluid on a single pore, thus demonstrating proof of concept. It should then have broader implications for numerous other problems and application domains. Our data-driven physics-informed inference framework can spur a more efficient, rational and systematic study of fluid-substrate interactions across a wide spectrum of subjects, including but not limited to, adsorption, capillarity and wettability.
Sessile drops and bubbles with characteristic dimensions on the nanometre scale play a central role in a wide spectrum of applications, from inkjet printing and vapour–liquid–solid growth processes to micro-/nanofluidics and the design and operation of lab-on-a chip devices. But their theoretical understanding remains incomplete and several fundamental aspects still elude us. This is largely due to the challenging physics of such small objects, often revealing sensitive dependence on the nature of the intermolecular forces, surface wetting properties and interface fluctuations.
In this study, we use classical density functional theory (DFT) to consistently incorporate the existence of the surface phase transitions, particularly the prewetting transition, and uncover their effects on the formation and stability of nanodrops and nanobubbles. This allows us to identify thermodynamic accessibility regions of nanodrops and nanobubbles adsorbed on flat walls. Using DFT we propose a method for computing the interface binding potential, which is based on computing the work of adsorbate formation from the free energy functional. Full unconstrained minimisation of DFT allows us to capture the correct long-ranged asymptotes of the density profiles, which are known to affect the binding potential. It also allows us to treat liquid and gas adsorption consistently within the same framework and uncover a very intriguing relationship between film adsorption and drop/bubble formation.
Fully microscopic DFT computation of nano-drops/bubbles (colour) against a properly calibrated macroscopic model of thin films (black lines).
We found that the regions in the thermodynamic space of temperature and chemical potential where nanodrops and nanobubbles exist are demarcated by the spinodals of planar wetting films. Remarkably, this implies that surface nanobubbles may be more amenable to experimental study than nanodrops, precisely because they occupy a bigger portion of the phase plane. Additionally the thin film spinodals can be used to compute the minimal radii of surface drops and bubbles.
One of our key findings is that the prewetting transition enables stabilisation of drops of liquid on vanishingly small impurities on the substrate. Certainly, this prompts the existence of a similar relation for low-temperature layering transitions. Investigating these effects is certainly of interest in future work and requires using a repulsive functional with a fully non-local treatment of repulsions.
The Cahn-Hilliard (CH) equation is a popular phase-field model initially proposed to describe the process of phase separation in binary alloys. Since then, it has found innumerable applications, from capillarity–wetting phenomena and diblock copolymer molecules to tumour growth, image inpainting and topology optimization. Like all phase-field models, the CH equation avoids the explicit treatment of sharp interfaces altogether via thin transition regions through which pertinent variables and physical properties vary rapidly but continuously.
We propose finite-volume schemes for the Cahn-Hilliard equation which unconditionally and discretely preserve the boundedness of the phase field and the dissipation of the free energy. Our numerical framework is applicable to a variety of free-energy potentials, including Ginzburg-Landau and Flory-Huggins, to general wetting boundary conditions, and to degenerate mobilities. Its central thrust is the upwind methodology, which we combine with a semi-implicit formulation for the free-energy terms based on the classical convex-splitting approach. The extension of the schemes to an arbitrary number of dimensions is straightforward thanks to their dimensionally split nature, which allows to efficiently solve higher-dimensional problems with a simple parallelization. The numerical schemes are validated and tested through a variety of examples, in different dimensions, and with various contact angles between droplets and substrates.

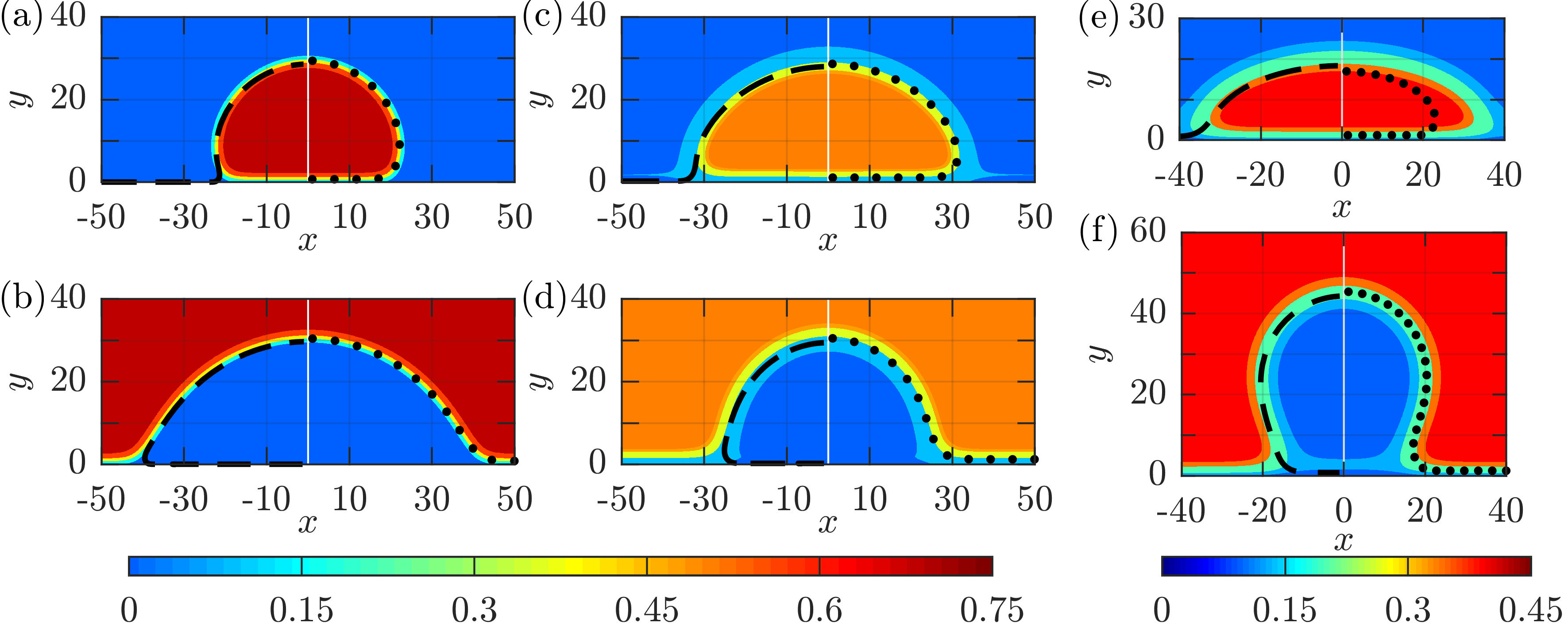
Numerical experiment of wetting phenomena with sessile droplets on a flat solid substrate. In this application a fluid-fluid interface moves along the solid substrate, while a contact line is formed at the intersection between the interface and the substrate. The figure represents the contour plots of stationary states of droplets on a substrate for differente contact angles (β) between the droplet and substrate. φ is the phase-field function, which describes the phase of the system with the limiting values φ = 1 and φ = -1 representing the two phases. The theoretical contact angles are shown by the dashed red lines, demonstrating good agreement with the simulated scheme.
This study builds naturally from our previous works aimed at designing structure-preserving finite-volume schemes for gradient flows and hydrodynamic systems, where a general free energy containing nonlocal interaction potentials drives the temporal evolution towards a steady state dictated by the minimizer of such free energy.
You can see the simulations of this project in the following link.