Harnessing control of a hidden world: from microfluidic mixing to polymer directed assembly
Electrohydrodynamics videos
Electrohydrodynamics 1
Electric field manipulation of the Rayleigh-Taylor instability in an unconfined geometry wherein progressively stronger voltages are applied going from left to right, to the point of complete suppression of the instability.
Electrohydrodynamics 1
Electric field manipulation of the Rayleigh-Taylor instability
Electric field manipulation of the Rayleigh-Taylor instability in an unconfined geometry wherein progressively stronger voltages are applied going from left to right, to the point of complete suppression of the instability.
Electrohydrodynamics 2
Electric field manipulation of the Rayleigh-Taylor instability
Evolution of the Rayleigh-Taylor instability for a thin liquid film resting above air inside a small scale confined geometry.
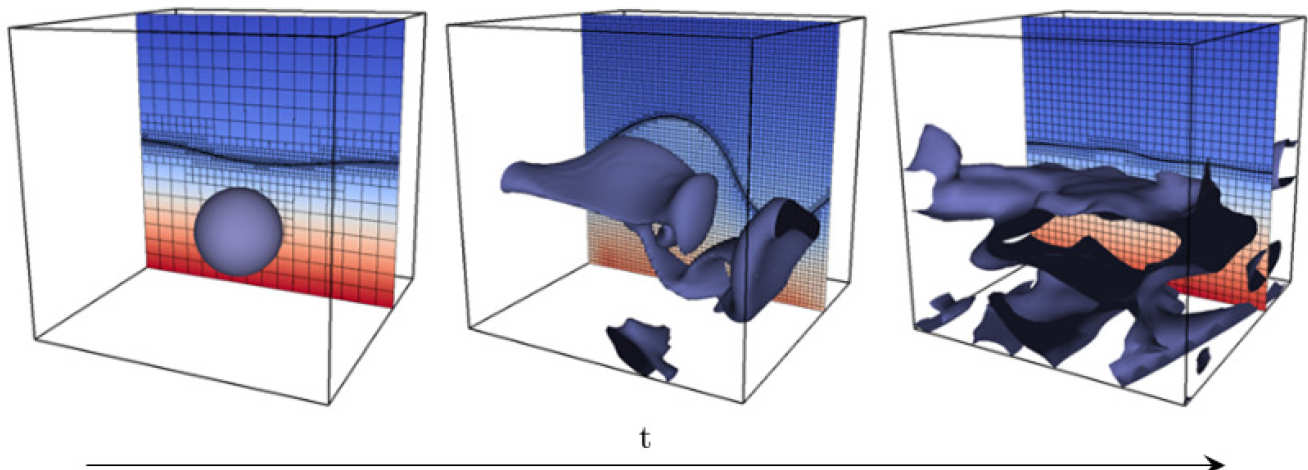
Electrohydrodynamics 3
Electric field manipulation of the Rayleigh-Taylor instability
Evolution of the Rayleigh-Taylor instability for a thick liquid film resting above air inside a small scale confined geometry.
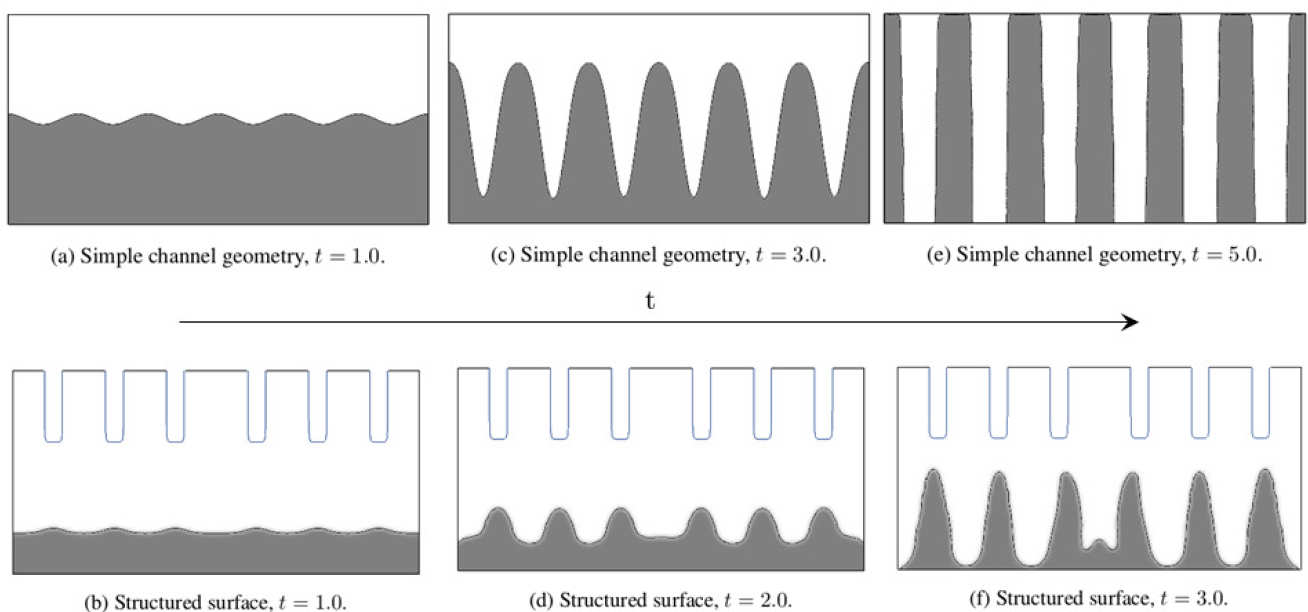
Electrohydrodynamics 4
Directed assembly topography
Directed assembly using electric fields in a domain with surface topography.
Fluid dynamics at small scales is at the forefront of modern research. And now more than ever we can benefit from advances that lie at the tip of our fingers. With sizes not exceeding a few millimetres and usage ranging from blood sample analysis to cooling devices and tiny integrated circuit components (and far beyond), liquid systems on the microscale play an indispensable part in our lives. Their production and maintenance however is a highly sensitive and expensive process. Many classical implementations take into account intricate geometries and complex networks of channels to reach their targets. Furthermore, the presence of injected flows in such small scales is often invasive and prevents optimisation and scaling towards industrially efficient standards.
Our research focuses on eliminating these drawbacks and creating mechanisms that do not use any moving parts and do not require the presence of an oncoming flow. How would the fluid move then? Electrostatic control mechanisms underpin a wide range of modern industrial processes, from lab-on-a-chip devices to microfluidic sensors for security applications. We analyse electrostatic control procedures in simple geometrical configurations, such as channels containing layers of immiscible fluids. Stability theory guides the imposition of voltage distributions that efficiently manipulate the fluid-fluid interface and harness the classical instabilities arising in such systems (Physics of Fluids, 2014). We then formulate nonlinear asymptotic models that enable the study of the interfacial motion far beyond the level of small perturbations (Physical Review Fluids, 2017).
We have developed theoretical and numerical tools that allow us to study the flow environment on the microscale in a virtual computational laboratory, thus eliminating the need for costly experiments. We use this knowledge to design electric field protocols that target microfluidic mixing (International Journal of Multiphase Flow, 2015), flux generation (Proc. Royal Society, 2014) and directed polymer assembly in simple geometrical configurations where this has not been achieved before. The work is an excellent example of the fusion between state of the art mathematics, technology and high-impact high-risk applications.