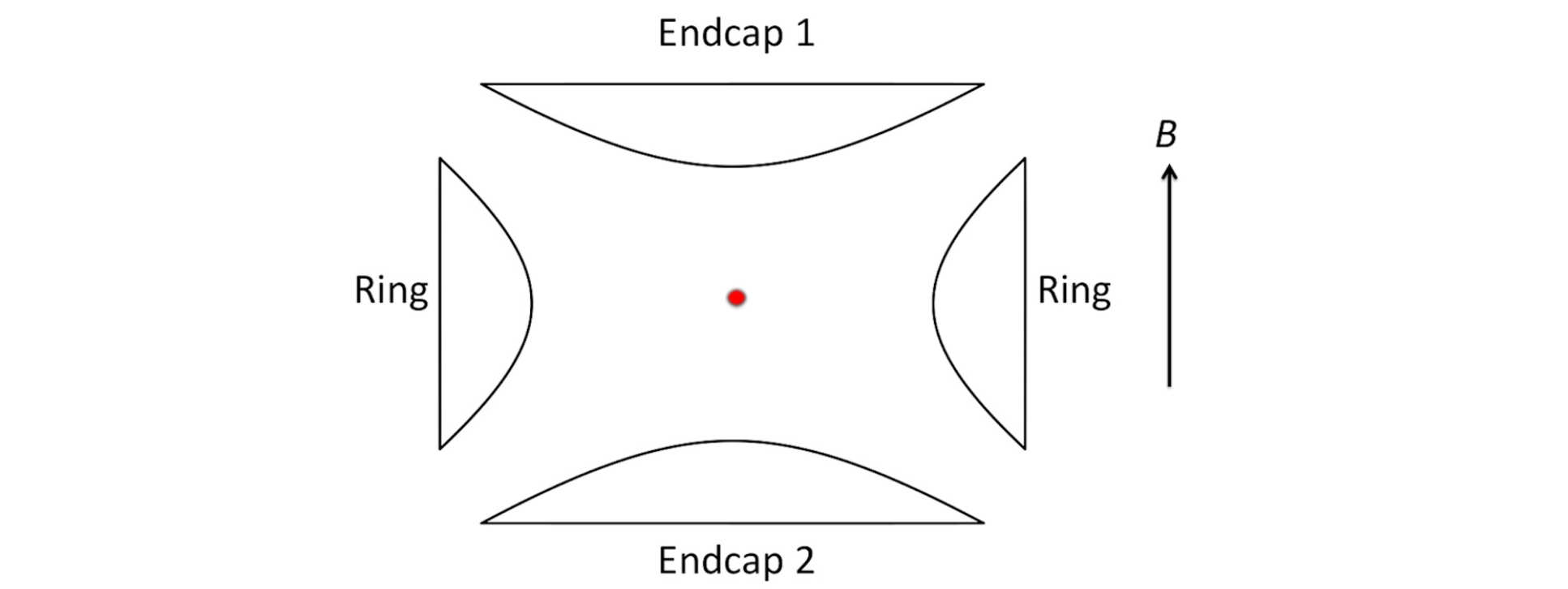
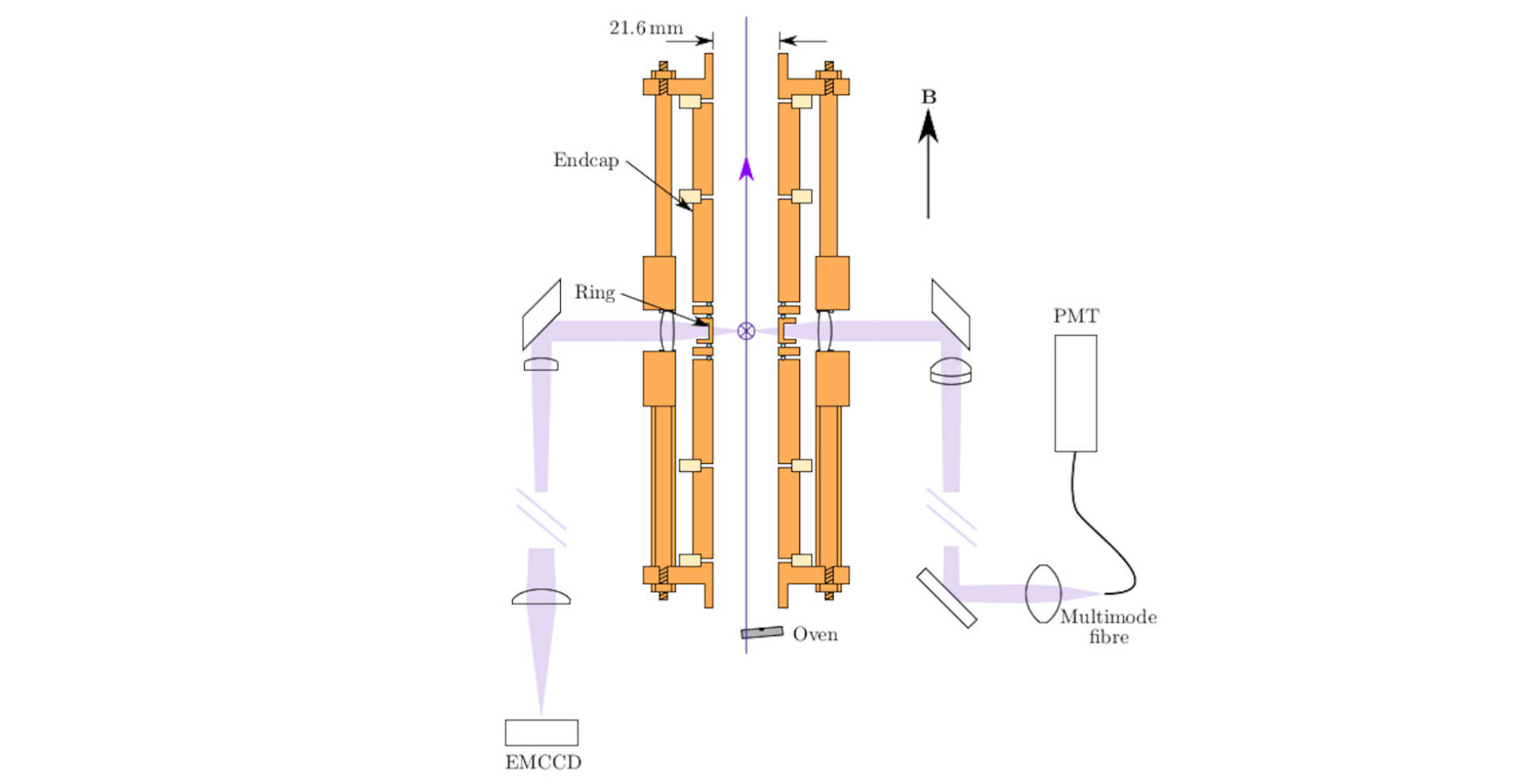
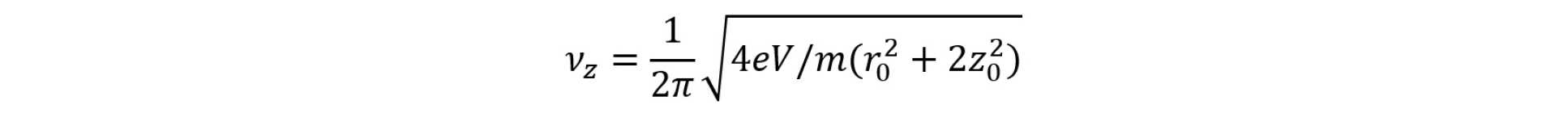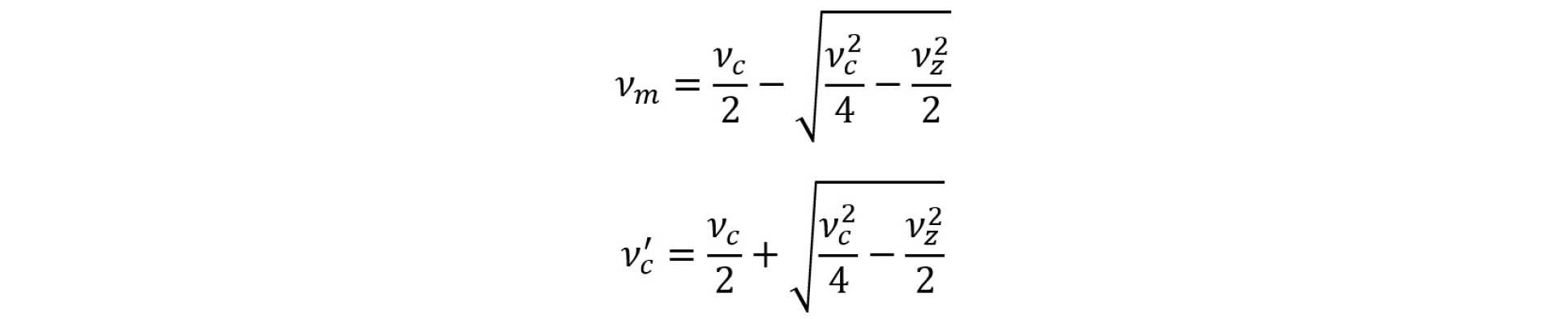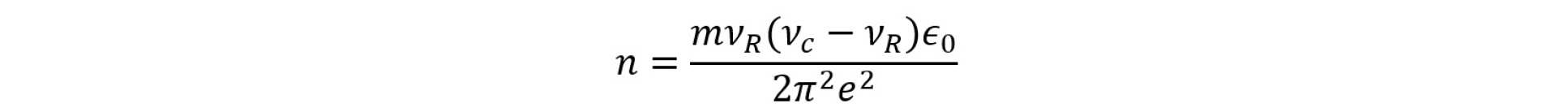Oscillation frequencies in the Penning trap
If the two endcap electrodes have a separation of 2z0 and the ring has an internal diameter of 2r0, the axial oscillation frequency of a single ion is given by
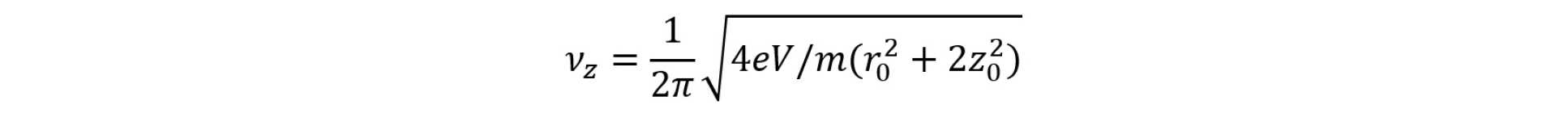
where V is the applied potential between endcaps and ring, and e and m are the charge and mass of the ion respectively.
The magnetron and modified cyclotron frequencies are given by:
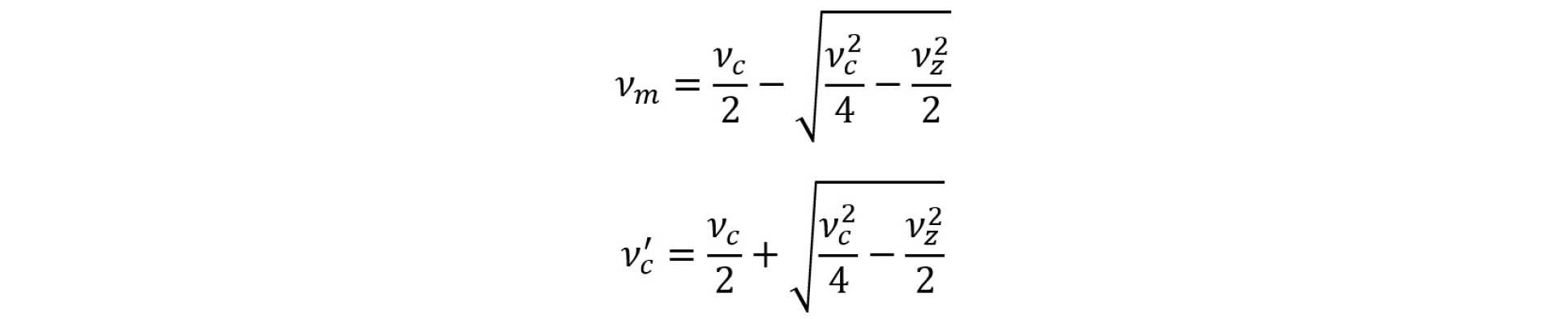
where the unperturbed cyclotron frequency is given by vc = eB/m. Here, B is the magnetic field strength.
If more than one ion is trapped, these equations describe the oscillation frequencies of the centre of mass (COM), and there are additional degrees of freedom corresponding to internal modes of the cloud of ions, i.e. the relative motion of the ions. In particular, in equilibrium the whole ion cloud generally rotates uniformly at a frequency given by νR, which can take any value between νm and ν’c. This rotation frequency is related to the density of ions in the trap through the equation
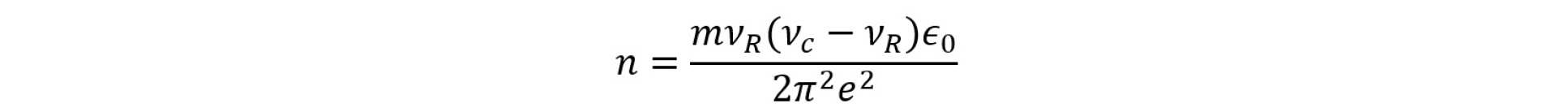
See Ref. [1] for more details. For a small number of ions that have formed an ion Coulomb crystal, there are well-defined modes of oscillation for the internal motion.