Research

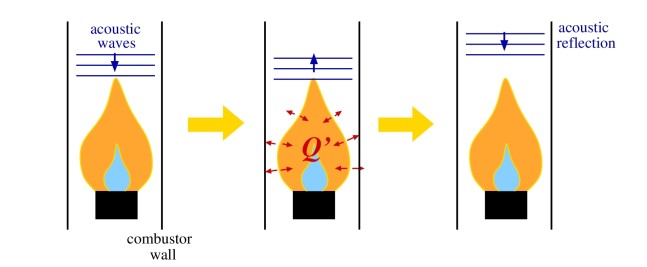
Thermoacoustic instability, also known as combustion instability, is caused by a two-way coupling between acoustic waves and unsteady heat release.

For example, unsteady heat release from a flame generates acoustic waves. These propagate within the combustor, reflect from boundaries and arrive back at the flame, where they generate more unsteady heat release. The cycle may repeat, leading to successively increasing amplitudes - thermoacoustic instability.

Thermoacoustic instabilities are noisy and the resulting vibration can severely damage the gas turbine.

They are a long-standing and very serious problem as they are the key barrier to low NOx emissions from aero-engines and power station gas turbines.

The very combustion conditions which are needed for low NOx emissions (lean premixed combustion) can't be properly achieved due to their propensity to thermoacoustic instability.

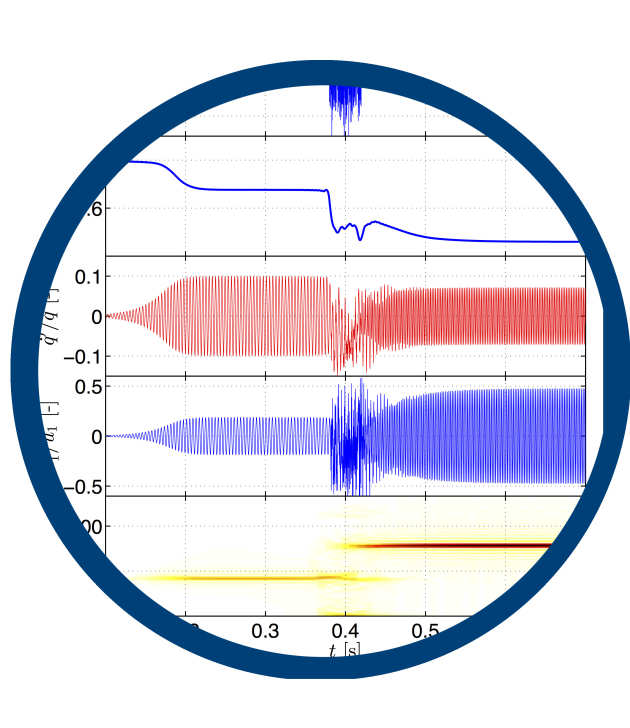Our research aims to improve understanding and prediction of thermoacoustic instability. We are especially interested in multi-scale prediction methods which:

• treat the generation and propagation of acoustic waves using low-dimensional, linear modelling methods.
• treat the unsteady response of the flame to acoustic perturbations using high-fidelity simulations.

These treatments are then coupled, resulting in highly efficient computational prediction. Our group has developed a low order network modelling tool which implements this coupled approach. It models a complicated combustor geometry as a series of connected simple geometry modules, with acoustic boundary conditions applied at either end.

A variety of flame models can be prescribed or imported, allowing the frequencies and amplitudes of thermoacoustic oscillations to be predicted. Our resulting code, OSCILOS (Open Source Combustion Instability Low Order Simulator), is freely available and can be found at www.oscilos.com.

We are also researching methods of suppressing instability using both active (feedback) and passive control, including developing improved acoustic models for the damping effects of holes, liners and Helmholtz resonators.

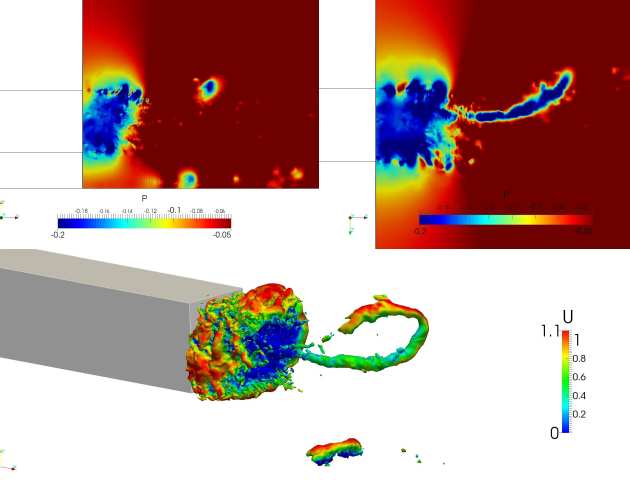At motorway/highway speeds, over half of the fuel burnt by a road vehicle is used to overcome aerodynamic drag. The main contributor to aerodynamic drag is pressure drag, also known as form drag.

This arises due to the separation of the flow over the rear of the vehicle, forming a low pressure wake region. 

We are investigating the wake flows behind simplfiied road vehicles., with particular current focus on the wake asymmetries that occur.

We are also investigating the use of feedback control to improve the pressure recovery, hence reducing the pressure drag. As the location of the flow separation is essentially fixed, any feedback control must achieve drag reduction by altering the wake behind the body, rather than changing the separation location.

In practice, feedback control involves forcing actuators (such as slot jets or small flaps) located at the rear of the vehicle in response to pressure readings. This work is both computational, using Large Eddy Simulations. and experimental, using wind tunnel experiments.