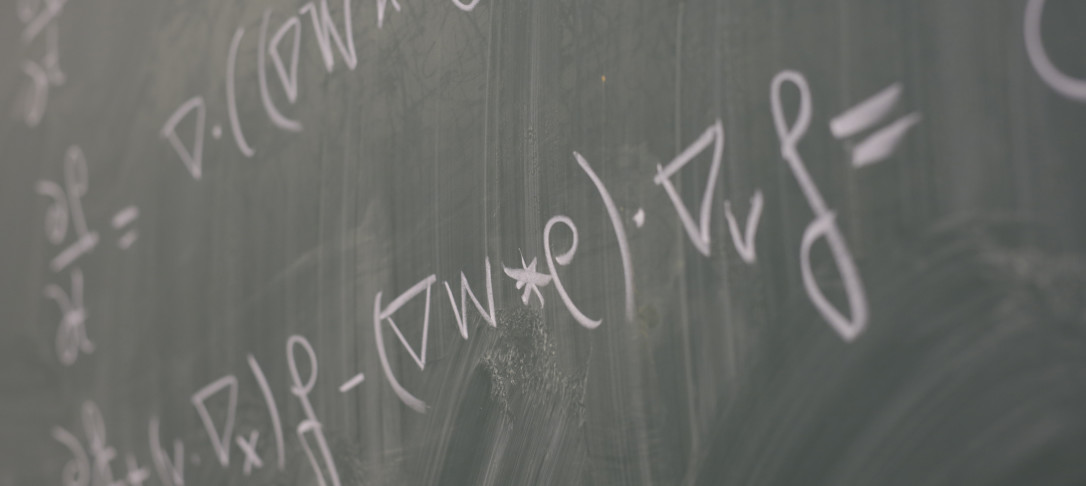
Title
Quantitative De Giorgi methods in kinetic theory for non-local operators
Abstract
We derive quantitatively the Harnac inequalities for kinetic integro-differential equations. This implies Hölder continuity. Our method is based on trajectories and exploits a term arising due to the non-locality in the energy estimate. This permits to quantitatively prove the intermediate value lemma for the full range of non-locality parameter s\in (0,1). The Strong Harnack inequality follows by non-probabilistic methods. Our results apply to the inhomogeneous Boltzmann equation in the non-cutoff case.
Please note that the seminar will take place in person in room 658 of Huxley Building.