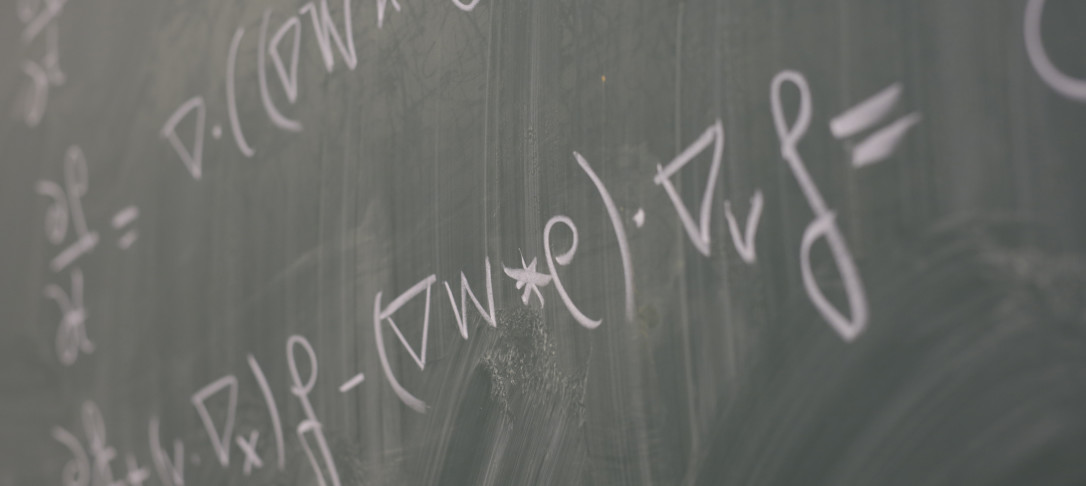
Title
On energy conservation for the hydrostatic Euler equations: an Onsager Conjecture
Abstract
Onsager’s conjecture states that weak solutions of the incompressible Euler equations conserve kinetic energy (the L^2 norm in space) if the velocity field is Hölder continuous in space with exponent bigger than 1/3. In case the exponent is less than 1/3 energy dissipation can occur. We consider an analogue of Onsager’s conjecture for the hydrostatic Euler equations (also known as the inviscid primitive equations of oceanic and atmospheric dynamics). These equations arise from the Euler equations under the assumption of the hydrostatic balance, as well as the small aspect ratio limit (in which the vertical scale is much smaller compared to the horizontal scales). Unlike the Euler equations, in the case of the hydrostatic Euler equations the vertical velocity is one degree spatially less regular compared to the horizontal velocities. The fact that the equations are anisotropic in regularity and nonlocal makes it possible to prove a range of sufficient criteria for energy conservation, which are independent of each other. This means that there probably is a ‘family’ of Onsager conjectures for these equations. This is joint work with Simon Markfelder and Edriss S. Titi.
Please note that the seminar will take place in person in room 140 of Huxley Building.