Aleksandra Bozovic — Introduction to quasiconformal maps (Junior Geometry Seminar)

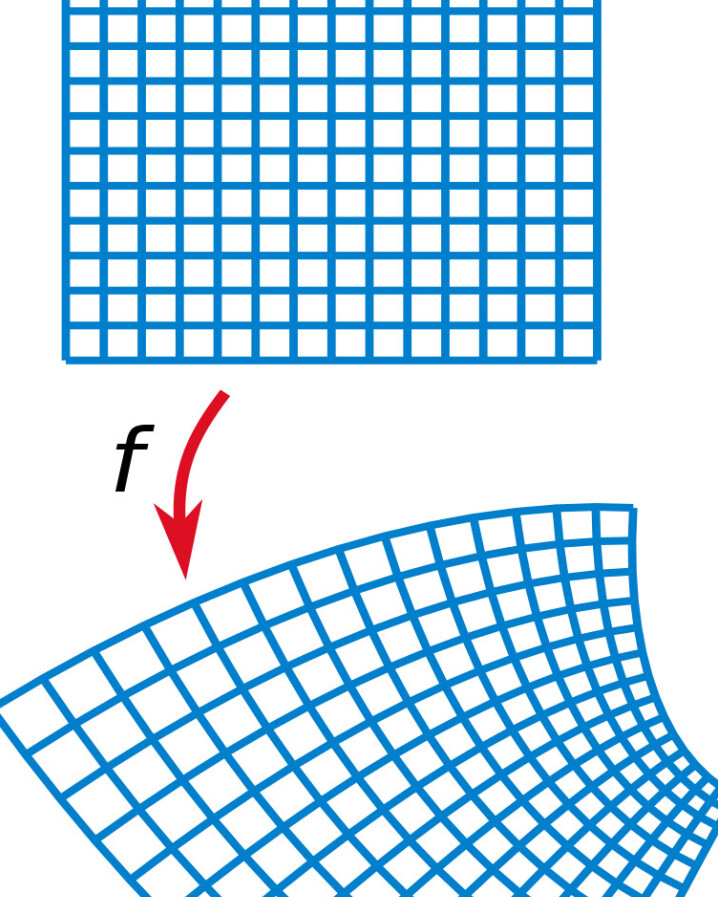
Abstract: Quasiconformal maps are closely related to conformal maps and share many of their nice properties, though they are less rigid, for example, they can be glued together and need not even be differentiable everywhere. They have applications in complex analysis, complex dynamics and mathematical physics. I shall present various equivalent definitions of quasiconformal maps, their basic properties, and their relation to almost complex structures, which shall include a visual intuition for almost complex structures on surfaces, and a proof of the Newlander-Nirenberg theorem in this basic case.