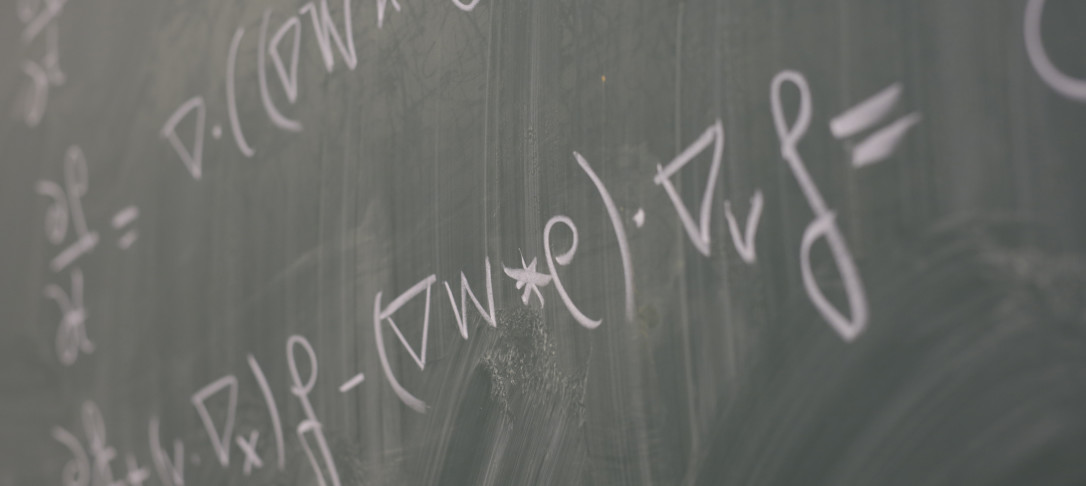
Title
The Stochastic Heat Equation with time correlation
Abstract
We consider the multiplicative Stochastic Heat Equation
in the critical dimension d = 2 with a Gaussian random potential. We
will focus in the case where the potential is not white in time and we will study the large scale fluctuations
of the solution. This case was considered before in d ≥ 3 where it was proved that the
fluctuations converge to the Edwards-Wilkinson limit with a nontrivial effective diffusivity and an effective
variance. We prove that this result can be extended to d = 2. In particular we show that after tuning the noise strength in a critical way and renormalizing the large scale fluctuations of the solution, they converge in distribution to the
Edwards-Wilkinson model with an explicit effective variance but with a trivial effective diffusivity. Our main tools is
the Feynman-Kac formula and a fine analysis of a specific Markov chain on the space of paths that was first
introduced in d ≥ 3 for the same problem.
Please note that the seminar will take place in person in room 140 of Huxley Building.