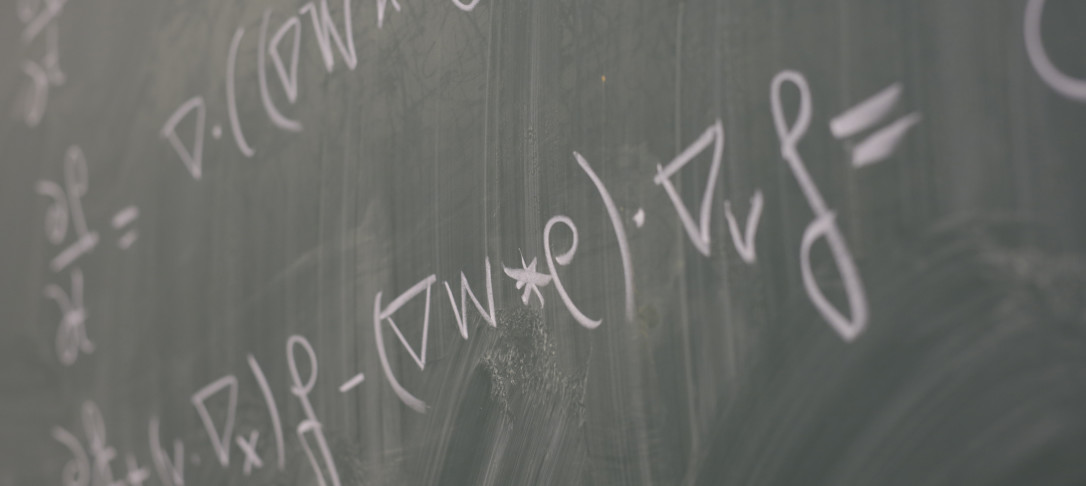
Title
Stabilizing control and deflation for the McKean–Vlasov PDE
Abstract
In the context of interacting particle systems, collective behavior is often described at the mean-field level by the time evolution of a probability density distribution governed by McKean–Vlasov-type equations. The system’s emergent patterns, based on the underlying microscopic interactions, are represented in terms of stationary states of the evolutionary partial differential equation (PDE). A common feature of these systems is the coexistence of various steady configurations and non-trivial phase transitions. The nature and number of steady states are linked to two key parameters: the bath temperature (noise amplitude) and the interaction strength, measuring the interplay between diffusivity and drift, in addition to the modeling of the forces acting on the particle ensemble.
To capture the different steady states of the McKean–Vlasov equation, a Spectral Galerkin approximation is combined with a deflated Newton’s method, factoring out roots as they are identified. Comparison with existing asymptotic analysis results allows for the verification of solutions and the classification between stable and unstable configurations. Once the steady states are found, an optimal control problem is designed to stabilize the system at a desired unstable steady state. The control action is computed via iterated open-loop solves in a receding horizon fashion. The proposed numerical procedure is particularly interesting when dealing with dynamics naturally leading to consensus or concentration profiles, where the control objective could be the promotion of chaos and the prevention of clustering.
Please note that the seminar will take place in person in room 144 of Huxley Building.