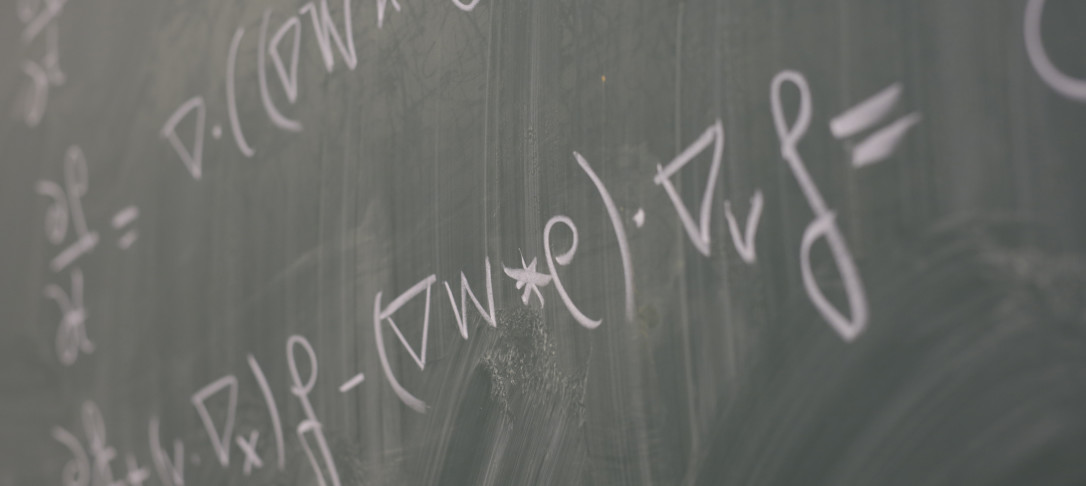
Title
On absence of embedded eigenvalues and stability of BGK waves
Abstract
We consider space-periodic and inhomogeneous steady states of the one-dimensional electrostatic Vlasov-Poisson system, known as the Bernstein-Greene-Kruskal (BGK) waves. We prove that there exists a large class of the fixed background ion densities and spatial periods, so that the corresponding linearised operator around the associated BGK-equilibria has no embedded eigenvalues inside the essential spectrum. As a consequence we conclude a nonquantitative version of Landau damping around a subclass of such equilibria with monotone dependence on particle energy.
Please note that the seminar will take place in person in room 144 of Huxley Building.