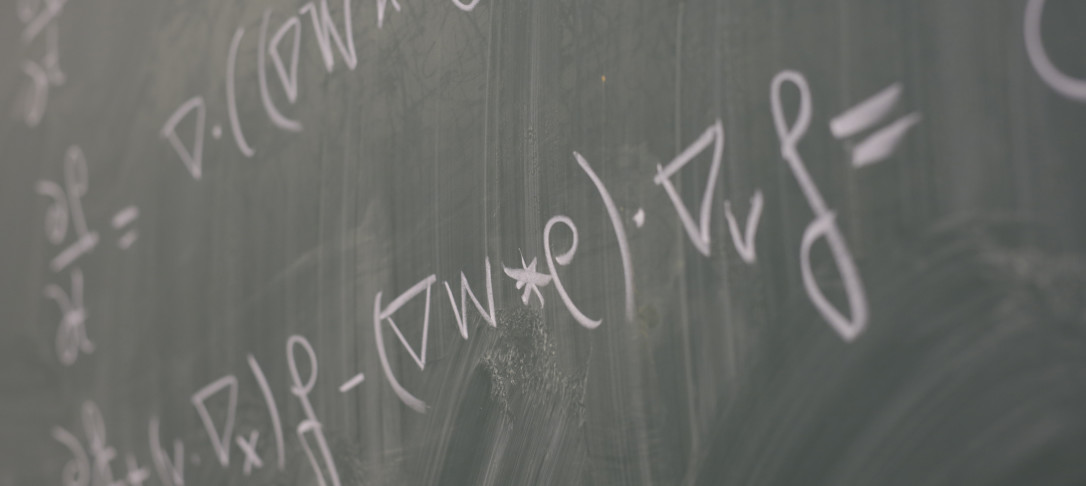
Title
The Index of CMC Surfaces in Three-Manifolds
Abstract
CMC surfaces are certain geometric variational objects, and their index is a measure of their instability (the greater the index, the greater the instability). On the one hand, geometrical examples illustrate that a certain general estimate on the index of CMC surfaces by their mean curvature, area, and genus should hold. On the other hand, from an analytical point of view, computing the index of a CMC surface boils down to computing the index of a certain Schrödinger operator; moreover, when the domain has dimension at least three, there is a broad and general theory that would prove the aforementioned geometrically motivated estimate. However, when the domain is two-dimensional (as is the case here), standard examples show that this broad and general theory cannot hold, so that this geometrically motivated estimate cannot be established by these methods. Nevertheless, by exploiting the geometric two-dimensional nature of the problem, we can overcome this obstacle and indeed establish the above estimate. This is joint work with Ben Sharp.
Please note that the seminar will take place in person in room 144 of Huxley Building.