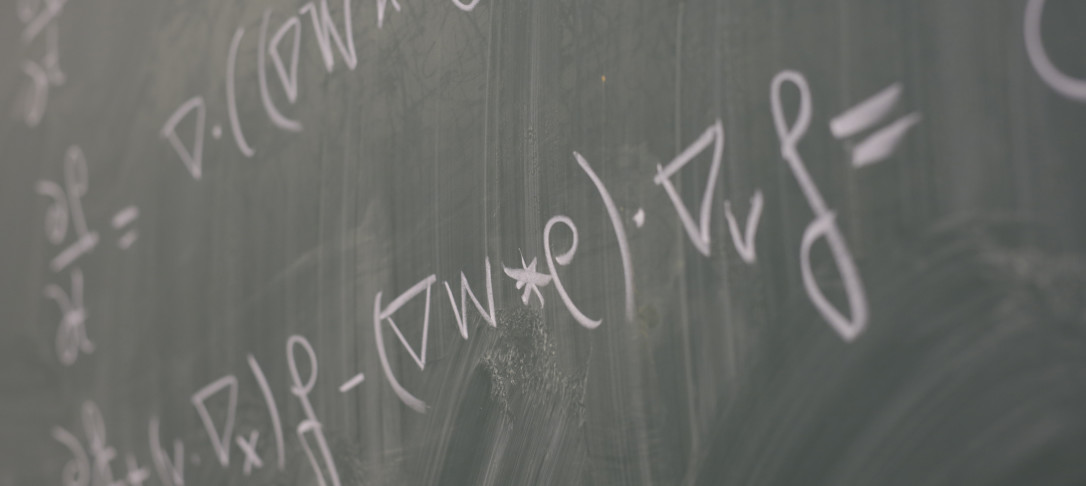
Title
Sharp spectral projection estimates for the torus
Abstract
It is a natural, but oftentimes difficult, question to deduce information about a periodic function from its Fourier series expansion. Spectral projection estimates are one way to explore this connection. If a function has its spectrum contained in an annulus, how large can the function be in an L^p norm? For unit width annuli this question is answered by the universal estimates of Sogge. If the projection operator projects onto an eigenspace, this is the Discrete Restriction conjecture of Bourgain. We present sharp estimates for intermediate cases for a large subset of the relevant parameters, which addresses a conjecture of Germain and Myerson. We will discuss the techniques used, similarities and differences to the case of general manifolds, and potential future avenues of attack.
Please note that the seminar will take place in person in room 144 of Huxley Building.