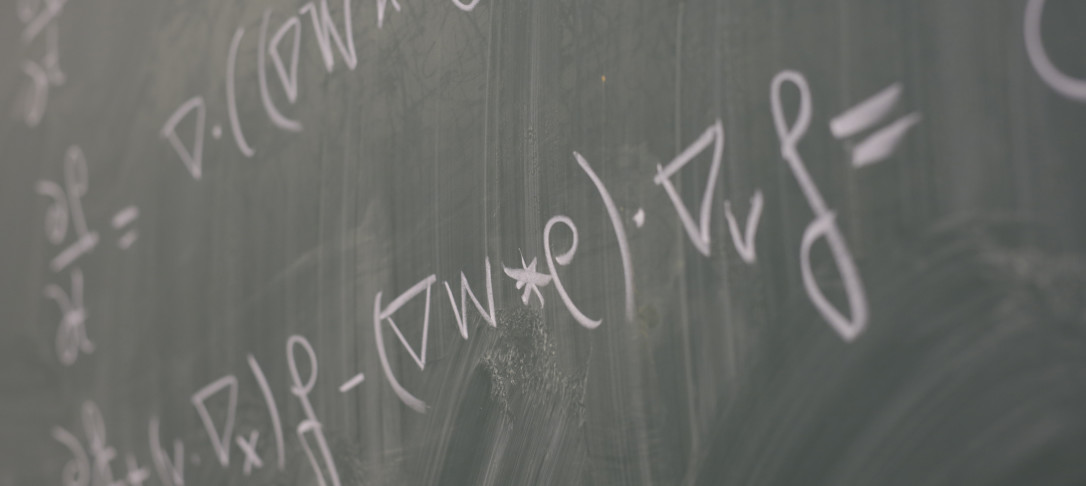
Title
Global well-posedness of a 2D fluid-structure interaction problem without dissipation
Abstract
In this talk, we will analyze the incompressible Euler equation in a time-dependent 2D fluid domain, whose interface evolution is governed by the law of linear elasticity without damping. Our main result asserts that the Cauchy problem is globally well-posed in the energy space for irrotational initial data without any smallness assumption. We also prove the continuity with respect to the initial data and the propagation of regularity. In the absence of parabolic regularization, a key ingredient in our analysis is a novel reduction to a nonlinear Schrödinger-type equation, allowing us to apply dispersive estimates. To carry this out, we develop new estimates for the Dirichlet-to-Neumann operator in low-regularity regimes through tools from classical harmonic analysis and paradifferential calculus. This is a joint work with Thomas Alazard and Chengyang Shao.
Please note that the seminar will take place in person in room 144 of Huxley Building.