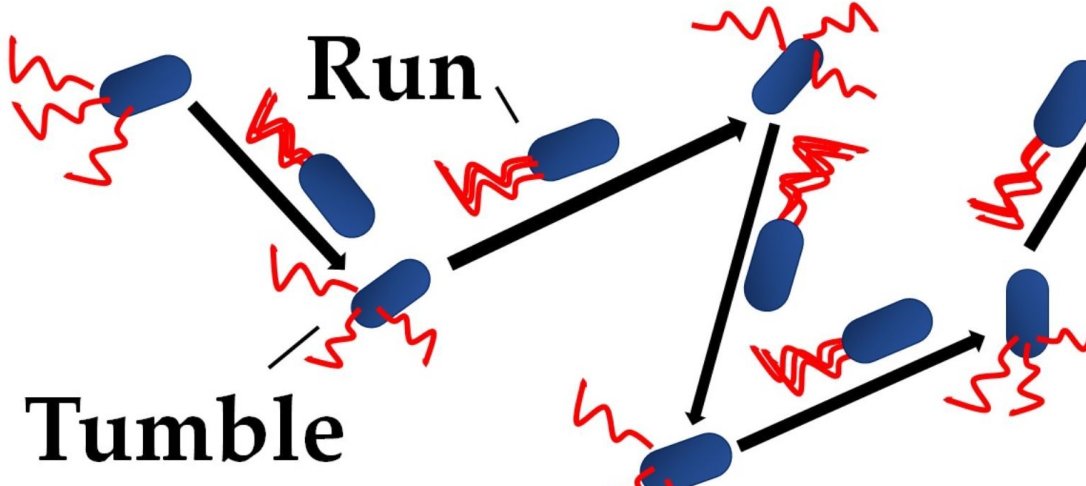
I will present work on current fluctuations in stochastic processes with resetting, demonstrating in particular how phase transitions in the large deviations can be understood via a mapping to the classic Poland-Scheraga model for DNA denaturation [R. J. Harris and H. Touchette, J. Phys. A: Math. Theor. 50, 10LT01 (2017)].  This approach can be extended to treat the case where the dynamics between resets depends on the value of a parameter fixed at the last reset and in this context I will discuss applications to run-and-tumble models of bacterial dynamics.

Finally, I will mention the recent development of a “Thermodynamic Uncertainty Relation” which applies for such run-and-tumble–type processes [M. Shreshtha and R. J. Harris, EPL (Europhysics Letters) 126, 40007 (2019)].