Floquet engineering & time crystals
by Derek Lee
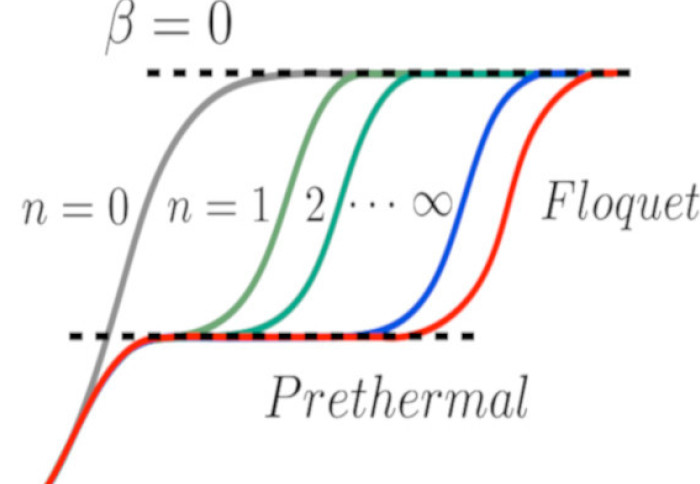
Pre-thermal plateau in entropy growth
Periodically driven systems does not simply heat up. Pre-thermal states exist with novel forms of non-equilibrium order, "time crystals".
Generic quantum many-body systems subject to time dependent drives generally absorb energy heating to the featureless infinite temperature state. However, it is by now well established, both rigorously and numerically, that for periodically driven (Floquet) systems a long-lived transient prethermal regime can appear in the high frequency limit. This perthermal regime lies at the heart of Floquet-engineering sought-after Hamiltonians and may even host novel forms of non-equilibrium order, most prominently discrete time crystals.
A natural next step is to go beyond fully periodic drives to protocols where the perfect periodicity is explicitly broken, for instance, in quasi-periodic or even random drives. In our works, we address the basic question whether prethermalization can appear for aperiodically driven many-body systems.
In Ref. [1], we introduce a family of random multipolar drives (RMD) which interpolates between highly structured Thue-Morse quasi-periodic and fully random driving. We show numerically that prethermal plateaus similar to the celebrated case of Floquet systems can emerge. The prethermal lifetime exhibits a power law scaling which we explain by a simple Fermi’s golden rule calculation. Crucially, we establish that the prethermal regime of randomly driven systems may also host non-equilibrium phases which we illustrate with a novel random discrete time crystal.
In Ref. [2], we derived rigorous and non-perturbative bounds on the heating rate for the Thue-Morse quasi-periodic driving and the RMD for generic quantum many-body systems. For Thue-Morse quasi-periodic driving, our bound shows an unexpected dependence on the frequency: the heating rate vanishes faster than any polynomial but slower than exponential as the frequency increases. Such a dependence is unfamiliar but in agreement with our numerical simulation.
Rigorous statements about non-equilibrium many-body dynamics are rare, especially for drives without perfect periodicity. Therefore, our work thus solves a crucial problem and opens a new avenue in the field of non-equilibrium many-body quantum systems. The prethermal phenomenon is of direct experimental relevance, i.e. for driven cold atomic gases and potentially even for quantum materials. Our works are of general interest for many communities, particularly to those concerned with thermalization, non-equilibrium quantum phases and quantum information processing.
[1] Zhao, H., Mintert, F., Moessner, R., & Knolle, J. (2021). Random multipolar driving: tunably slow heating through spectral engineering. Physical Review Letters, 126, 040601.
[2] Mori, T., Zhao, H., Mintert, F., Knolle, J., & Moessner, R. (2021). Rigorous bounds on the heating rate in Thue-Morse quasiperiodically and randomly driven quantum many-body systems. Physical Review Letters, 127, 050602
Article text (excluding photos or graphics) © Imperial College London.
Photos and graphics subject to third party copyright used with permission or © Imperial College London.
Reporter
Derek Lee
Department of Physics