Sum-Of-Squares Approach to Global Stability and Control of Fluid Flows
Уголок студента
Эту страницу ведет Людмила Чернышенко, студентка первого курса Математико-механического факультета Санкт-Петербургского государственного Университета. Рассказ о проекте на этой странице - для студентов.
Начнем с идеи:
Разложение многочлена в сумму квадратов
На этой странице мы дадим краткое описание метода разложения многочленов в суммы квадратов, открытого Пабло Паррило в 2000 году [1], и покажем, как при помощи выпуклого программирования может быть проверено существование этого разложения.
Замечание: выпуклое программирование – раздел математического программирования, посвященный теории и методам решения задач минимизации выпуклых функций на выпуклых множествах, задаваемых системами равенств и неравенств.
Определение: для любого х ϵ Rn многочлен p(x) называется разложением в суммы квадратов, если существуют многочлены fi(x) i=1, … ,M такие, что
p(x)=![]()
Теорема: многочлен p(x) степени 2d может быть представлен в виде суммы квадратов тогда и только тогда, когда существуют положительно полуопределенная матрица Q и вектор одночленов Z(x), содержащий одночлены вида ax1r1x2r2...xnrn, где r1+...rn ≤ d такие, что p(x)=ZT(x)QZ(x).
В общем одночлены в Z(x) не обязательно алгебраически независимы. Вычислив ZT(x)QZ(x) и приравняв коэффициенты при получившихся одночленах соответствующим коэффициентам p(x), мы получаем набор аффинных отношений между элементами Q. Проблема нахождения положительно полуопределенной матрицы Q, элементы которой удовлетворяют полученным аффинным отношениям, может быть решена при помощи выпуклого программирования. Как только для p(x) найдется соответствующая положительно-полуопределенная матрица Q, будет доказано, что p(x) может быть представлен в виде суммы квадратов.
Справка:
- Самосопряженная матрица - квадратная матрица, элементы которой являются комплексными числами, и которая, будучи транспонирована, равна комплексно сопряжённой: AT=A. То есть, для любого столбца i и строки j справедливо равенство aij=aji.
- Самосопряжённая матрица A размерности n×n является положительно полуопределенной, если xTAx ≥0 для всех х ϵ Rn.
- Величина λ называется собственным числом квадратной матрицы А, а вектор x≠0 называется собственным вектором, если выполнено Ах=λx.
- Для самосопряженной матрицы все собственные числа вещественные, и существует ортонормированный базис e1,…,en такой, что e1,…,en являются ее собственными векторами. В этом базисе матрица А имеет диагональный вид
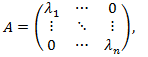 то есть aij=0 при i≠j, а λ1, … , λn - собственные значения матрицы A.
то есть aij=0 при i≠j, а λ1, … , λn - собственные значения матрицы A. - Диагональная матрица А положительно полуопределена тогда и только тогда, когда ее собственные значения неотрицательны. Для проверки данного утверждения достаточно рассмотреть выражение xTAx для произвольного x ϵ Rn:
хTАх=
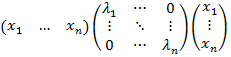 =
= 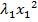 +…+
+…+ 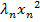 , причем выражение
, причем выражение  +…+
+…+  ≥0 только при
≥0 только при 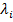 ≥0.
≥0. - Самосопряженная матрица положительно полуопределена тогда и только тогда, когда ее собственные значения неотрицательны (смотри утверждения 4 и 5).
Пример (из [2]): предположим, что мы хотим узнать, может ли многочлен четвертой степени p(![]() ) =
2
) =
2![]() +2
+2![]() -
-![]() +5
+5![]() , зависящий от двух переменных, быть представлен в виде суммы квадратов многочленов.
Для этого определим
Z(x)=
, зависящий от двух переменных, быть представлен в виде суммы квадратов многочленов.
Для этого определим
Z(x)=![]() Т
и рассчитаем следующую квадратичную форму:
Т
и рассчитаем следующую квадратичную форму:
p(![]() ) =
2
) =
2![]() +2
+2![]() -
-![]() +5
+5![]() = Z(x)Т
= Z(x)Т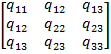 Z(x)
=
Z(x)
= ![]() +
+ ![]() +
+ ![]() +2
+2 ![]() +2
+2 ![]() .
.
Из этого равенства получаем следующие отношения:
![]()
![]()
![]()
![]()
![]() Теперь при помощи методов полуопределенного программирования мы можем найти
Теперь при помощи методов полуопределенного программирования мы можем найти
![]() и
и ![]() ,
удовлетворяющие последнему уравнению, такие, что матрица Q будет положительно полуопределена. Эти условия выполняются при
,
удовлетворяющие последнему уравнению, такие, что матрица Q будет положительно полуопределена. Эти условия выполняются при ![]() и
и ![]() .
Затем мы находим базис, в котором матрица Q будет иметь диагональный вид, и выражаем одночлены в векторе Z(x) через этот базис, перемножаем по формуле p(x)=Z(x)TQZ(x) и получаем следующее разложение в сумму квадратов:
.
Затем мы находим базис, в котором матрица Q будет иметь диагональный вид, и выражаем одночлены в векторе Z(x) через этот базис, перемножаем по формуле p(x)=Z(x)TQZ(x) и получаем следующее разложение в сумму квадратов:
p(![]() ) =
) = ![]() .
.
Замечание: Из того, что многочлен p(x) может быть представлен в виде суммы квадратов, следует, что многочлен p(x)≥0 для всех х ϵ Rn. Однако обратное утверждение не всегда верно. Не все неотрицательные многочлены могут быть представлены в виде суммы квадратов, за исключением трех случаев:
- n=2, т.е. пространство двумерное;
- deg(p)=2, т.е. степень многочлена p(x) равна двум;
- n=3 и deg(p)=4, т.е. пространство трехмерное и степень многочлена p(x) равна четырем.
Мы уже говорили, что положительно полуопределенная матрица, элементы которой удовлетворяют аффинным отношениям, может быть найдена при помощи методов выпуклого программирования, но для этого нам нужно убедиться, что множество, над которым мы хотим применить эти методы, является выпуклым.
Справка: Множество называется выпуклым, если оно вместе с любыми двумя своими точками, содержит в себе отрезок, соединяющий эти точки. Другими словами, множество G ϵ Rn называется выпуклым, если для любых двух точек x1 ϵ G, x2 ϵ G и для любого λ, 0≤λ≤1 верно, что λx1+(1-λ)x2 ϵ G. |
Для проверки выпуклости множества положительно полуопределенных матриц возьмем две матрицы, принадлежащие этому множеству, ![]() и проверим что матрица A=
и проверим что матрица A=![]() +
+![]() , где 0≤λ≤1, будет также положительно полуопределена. Для этого рассмотрим равенство xТAx= xТ
, где 0≤λ≤1, будет также положительно полуопределена. Для этого рассмотрим равенство xТAx= xТ ![]() +
+![]() )x, где 0≤λ≤1. В связи с положительной полуопределенностью матриц
)x, где 0≤λ≤1. В связи с положительной полуопределенностью матриц ![]() и указанными выше условиями на λ, мы получаем что xТAx≥0, а это и означает, что матрица A положительно полуопределена. Следовательно, это множество является выпуклым.
и указанными выше условиями на λ, мы получаем что xТAx≥0, а это и означает, что матрица A положительно полуопределена. Следовательно, это множество является выпуклым.
Затем, убедившись, что множество положительно полуопределенных матриц является выпуклым, мы будем рассматривать такие положительно полуопределенные матрицы, элементы которых удовлетворяют полученным нами ранее аффинным отношениям.
Эти аффинные отношения образуют гиперплоскость, поэтому искомая матрица будет лежать в сечении выпуклого множества положительно-полуопределенных матриц, образованной гиперплоскостью. Как известно это сечение будет выпуклым, поэтому проблема нахождения необходимой матрицы действительно может быть решена при помощи выпуклого программирования.
Информация, используемая на данной странице, опирается на материалы статьи [2].
1. P. A. Parrilo. Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization. PhD thesis, California Institute of Technology, Pasadena, CA, 2000.
2. A. Papachristodoulou and S. Prajna. A Tutorial on Sum of Squares Techniques for Systems Analysis. 2005 American Control Conference June 8-10, 2005. Portland, OR, USA.
Latest:
- The project has ended.
- Paolo Luchini visited us on February 2016.
- Mihailo Jovanovic and Armin Zade visited us during the two weeks 2-15 November 2015.
- All our postdocs secured positions which will allow them to contninue working in cooperation with us: Deqing Huang will be a full professor at the Southwest Jiaotong University, China, Davide Lasagna will be a Frontier Fellow at the Universiy of Southampton, UK, and Giorgio Valmorbida will move to a faculty position at the Supelec and Paris-Sud University, France. Well done!
- Next progress meeting on February 23.2015.
- Remote conference was held on 5.02.2015.
- Sergei was at UCLA attending the Mathematics of Turbulence programme. He gave two presentations about the project.
- Remote conference was held on 30.10.2014.
- Remote conference was held on 09.06.2014.
- A progress meeting was held at Imperial College on 27.03.2014.
- Charles Doering is at Imperial 25-27.03.2014 and in Oxford 27-28.03.2014 He is giving a talk on 26.03, see "Miscellaneous".
- Remote conference was held on 14.03.2014.
- Sergei gave a talk at the NeZaTeGiUs conference NeZaTeGiUs conference on 02.03.2014.
- Deqing went to China 26-30 December and gave a talk at a workshop organized by the State Key Laboratory of Industrial Control Technology, Zhejiang University, Hangzhou.
- Remote conference was held on 20.12.2014 The record is available from Sergei.
- Paul visited London and Oxford for two weeks in October, and took part in the project meeting on 21.10.
- Sergei gave a talk at ICNAAM 2013.
- Remote conference was held on 19.09.2013 The record is available from Sergei.
- Remore conferences were video recorded on 14.05, 06.06, 25.06, 11.07, 16.08, and 21.08.2013 The records are available for the members of the team from Sergei, but the records are not in the repository, to save space.
- July 2013. Deqing gave a talk at the School of Aeronautics and Astronautics, Zhejiang University, Hangzhou, China.
- June 5 and 6, 2013. Our remote conference was spread over 2 days this time.
- May 19-31, 2013. Sergei was in Stockholm, taking part in NORDITA Stability and Transition programme, and the follow-on SIG-33 workshop, where he gave a talk on using SoS in fluid dynamics.
- May 14, 2013. We had our first remote conference. It was interesting, and useful. Giorgio, Davide, and Deqing presented, and we all had a good chat.
- April 22, 2013. SVN repository for the project was created by Paul, hosted at ETH.
- Kick-off meeting on April 18 went fine.
- Paul is here!
- Paul Goulart will be visiting Imperial from April 15 to May 3.
- 30.03.2013 This website opens.
- 28.03.2013 Project mailing list created.
- 11-15.03.2013 Wynn visited Doering in Michigan. <
- 19.02.2013 Chernyshenko visited Southampton team.