About the project

This 3-year project is funded by EPSRC under the grants EP/J011126/1 (Imperial College London, the leading partner of the project), EP/J010537/1 (University of Oxford), and EP/J010073/1 (University of Southampton). The project also receives support in kind from Airbus Operation Ltd., ETH Zurich (Automatic Control Laboratory), University of Michigan (Department of Mathematics), and University of California, Santa Barbara (Department of Mechanical Engineering).

The stability analysis of fluid flows, typically modelled by nonlinear Partial Differential Equations, is of fundamental importance for understanding unsteadiness and turbulence as well as proposing active flow control algorithms. We will develop a new approach for stability analysis and control of fluid flows, based on a recent progress in the application of Sum of Squares of polynomials and semidefinite programming in combination with a Lyapunov-based approach to stability analysis and design. The results will be implemented on a rotating Couette flow.



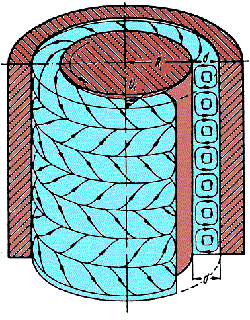
Rotating Couette flow has an iconic status in stability analysis. This flow is illustrated in the figure by a creative colouring of the picture from the iconic book by Hermann Schlichting (1979).

Latest:

  • The project has ended.
  • Paolo Luchini visited us on February 2016.
  • Mihailo Jovanovic and Armin Zade visited us during the two weeks 2-15 November 2015.
  • All our postdocs secured positions which will allow them to contninue working in cooperation with us: Deqing Huang will be a full professor at the Southwest Jiaotong University, China, Davide Lasagna will be a Frontier Fellow at the Universiy of Southampton, UK, and Giorgio Valmorbida will move to a faculty position at the Supelec and Paris-Sud University, France. Well done!
  • Next progress meeting on February 23.2015.
  • Remote conference was held on 5.02.2015.
  • Sergei was at UCLA attending the Mathematics of Turbulence programme. He gave two presentations about the project.
  • Remote conference was held on 30.10.2014.
  • Remote conference was held on 09.06.2014.
  • A progress meeting was held at Imperial College on 27.03.2014.
  • Charles Doering is at Imperial 25-27.03.2014 and in Oxford 27-28.03.2014 He is giving a talk on 26.03, see "Miscellaneous".
  • Remote conference was held on 14.03.2014.
  • Sergei gave a talk at the NeZaTeGiUs conference NeZaTeGiUs conference on 02.03.2014.
  • Deqing went to China 26-30 December and gave a talk at a workshop organized by the State Key Laboratory of Industrial Control Technology, Zhejiang University, Hangzhou.
  • Remote conference was held on 20.12.2014 The record is available from Sergei.
  • Paul visited London and Oxford for two weeks in October, and took part in the project meeting on 21.10.
  • Sergei gave a talk at ICNAAM 2013.
  • Remote conference was held on 19.09.2013 The record is available from Sergei.
  • Remore conferences were video recorded on 14.05, 06.06, 25.06, 11.07, 16.08, and 21.08.2013 The records are available for the members of the team from Sergei, but the records are not in the repository, to save space.
  • July 2013. Deqing gave a talk at the School of Aeronautics and Astronautics, Zhejiang University, Hangzhou, China.
  • June 5 and 6, 2013. Our remote conference was spread over 2 days this time.
  • May 19-31, 2013. Sergei was in Stockholm, taking part in NORDITA Stability and Transition programme, and the follow-on SIG-33 workshop, where he gave a talk on using SoS in fluid dynamics.
  • May 14, 2013. We had our first remote conference. It was interesting, and useful. Giorgio, Davide, and Deqing presented, and we all had a good chat.
  • April 22, 2013. SVN repository for the project was created by Paul, hosted at ETH.
  • Kick-off meeting on April 18 went fine.
  • Paul is here!
  • Paul Goulart will be visiting Imperial from April 15 to May 3.
  • 30.03.2013 This website opens.
  • 28.03.2013 Project mailing list created.
  • 11-15.03.2013 Wynn visited Doering in Michigan.
    • <
  • 19.02.2013 Chernyshenko visited Southampton team.